Point in Polygon Strategies

This is an early draft of the full article published in Graphics Gems IV, the citation is:

Haines, Eric, "Point in Polygon Strategies," Graphics Gems IV, ed. Paul Heckbert, Academic Press, p. 24-46, 1994.

(The full article is better, but I cannot find the final text on my machine.) The associated code for this article is available online.

Testing whether a point is inside a polygon is a basic operation in computer graphics. Graphics Gems presents an algorithm for testing points against convex polygons (Badouel 1990). This Gem provides algorithms which are from 1.6 to 9 or more times faster for convex polygons. It also presents algorithms for testing non-convex polygons and discusses the advantages and drawbacks of each. Faster, more memory intensive algorithms are also presented, along with an O(log n) algorithm for convex polygons. Code is included for the algorithms discussed.

Polygon definition

There are two different types of polygons we will consider in this Gem: convex and non-convex. If a number of points are to be tested against a polygon, it may be worthwhile determining whether the polygon is convex at the start and so be able to use a faster test. Another Gem (Schorn 1993) in this volume discusses ways of determining convexity.

Inside vs. Outside

One definition of whether a point is inside a region is the Jordan Curve Theorem. Essentially, it says that a point is inside a polygon if, for any ray from this point, there is an odd number of crossings of the ray with the polygon's edges (Figure 1). This definition means that some areas which are enclosed by a polygon are not considered inside. The center pentagonal area inside a star is classified as outside because any ray from this area will always intersect an even number of edges.

If the entire area enclosed by the polygon is to be considered inside, then the winding number is used for testing. This value is the number of times the polygon goes around the point. For example, a point in the center pentagonal area formed by a star has a winding number of two, since the outline goes around it twice. If the point is outside, the polygon does not wind around it and so the winding number is zero. Winding numbers also have a sign, which corresponds to the direction the edges wrap around the point.

Complex polygons can be formed using either polygon definition. A complex polygon is one that has separate outlines (which can overlap). For example, the letter "R" can be defined by two polygons, one consisting of the exterior outline, the other the inside hole in the letter. Most point in polygon algorithms can be easily extended to test multiple outline polygons by simply running each polygon outline through separately and keeping track of the total parity.

3D to 2D

In ray tracing and other applications the original polygon is defined in three dimensions. To simplify computation it is worthwhile to project the polygon and test point into two dimensions. One way to do this is to simply ignore one component. The best component to ignore is usually that which, when ignored, gives the largest area polygon. This is easily done by taking the absolute value of each component of the polygon plane's normal and finding the largest (Glassner 1989). The corresponding coordinates in the polygon are then ignored. Precomputing some or all of this information once for a polygon uses more memory but increases the speed of the intersection test itself.

While the above method is simple and quick, another projection may be useful when the polygon vertices are not guaranteed to lay on a single plane. While such polygons could be considered ill defined, they do crop up. For example, if a spline surface is tessellated into quadrilaterals instead of triangles, then the quadrilaterals are likely to be ill defined in this way. If a component is simply dropped, cracking can occur between such polygons when they are cast upon different planes.

One solution is to tessellate such polygons into triangles, but this may be impractical for a variety of reasons. Another approach is to cast all polygons tested onto a plane perpendicular to the testing ray's direction. A polygon might have no area on this plane, but the ray would miss this polygon anyway. Casting a polygon onto an arbitrary plane means having to perform a matrix transformation, but this solution does provide a way around potential cracking problems.

Bounding Areas

Point in polygon algorithms benefit from having a bounding box around polygons with many edges. The point is first tested against this box before the full polygon test is performed; if the box is missed, so is the polygon. Most statistics generated in this Gem assume this bounding box test was already passed successfully.

In ray tracing, Worley (Worley 1993a) points out that the polygon's 3D bounding box can be treated like a 2D bounding box by throwing away one coordinate, as done above for polygons. By analysis of the operations involved, it can be shown to be generally more profitable to first intersect the polygon's plane then test whether the point is inside the 2D bounding box rather than first testing the 3D bounding box. Other bounding box variants can be found in Woo (Woo 1992).

Crossings Test

One algorithm for checking a point in any polygon is the crossings test. The earliest presentation of this algorithm is Shimrat (Shimrat 1962), though it has a bug in it. A ray is shot from the test point along an axis (+X is commonly used) and the number of crossings is computed (Figure 1). Either the Jordan Curve or winding number test can be used to classify the point. What happens when the test ray intersects one or more vertices of the polygon? This problem can be ignored by considering the test ray to be a half-plane divider, with one of the half-planes including the ray's points (Preparata 1985, Glassner 1989). In other words, whenever the ray would intersect a vertex, the vertex is always classified as being infinitesimally above the ray. In this way, no vertices are intersected and the code is both simpler and speedier.

One way to think about this algorithm is to consider the test point to be at the origin and to check the edges against this point. If the Y components of a polygon edge differ in sign, then the edge can cross the test ray. In this case, if both X components are positive, the edge and ray must intersect and a crossing is recorded. Else, if the X signs differ, then the X intersection of the edge and the ray is computed and if positive a crossing is recorded.

MacMartin (MacMartin 1992) pointed out that for polygons with a large number of edges there are generally runs of edges which have Y components with the same sign. For example, a polygon representing Brazil might have a thousand edges, but only a few of these will straddle any given latitude line and there are long runs of contiguous edges on one side of the line. So a faster strategy is to loop through just the Y components as fast as possible; when they differ then retrieve and check the X components. Compared to the basic crossings test the MacMartin test was up to 1.8 times faster for polygons up to 100 sides, with performance particularly enhanced for polygons with many edges.

Other optimizations can be done for this test. Preprocessing the edge list into separate X and Y component lists, with the first vertex added to the end, makes for particularly tight loops in the testing algorithm. This is not done in the code provided so as to avoid any preprocessing or additional memory costs.

[Addenda: Joseph Samosky and Mark Haigh-Hutchinson submitted (unpublished) articles to Graphics Gems V. One idea these submissions inspired is a somewhat faster crossings test. By turning the division for testing the X axis crossing into a tricky multiplication test this part of the test became faster, which had the additional effect of making the test for "both to left or both to right" a bit slower for triangles than simply computing the intersection each time. The main increase is in triangle testing speed, which was about 15% faster; all other polygon complexities were pretty much the same as before. On machines where division is very expensive (not the case on the HP 9000 series on which I tested) this test should be much faster overall than the old code. Your mileage may (in fact, will) vary, depending on the machine and the test data, but in general I believe this code is both shorter and faster. Related work by Samosky is in: Samosky, Joseph, "SectionView: A system for interactively specifying and visualizing sections through three-dimensional medical image data", M.S. Thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 1993. The routine online is called the CrossingsMultiplyTest.]

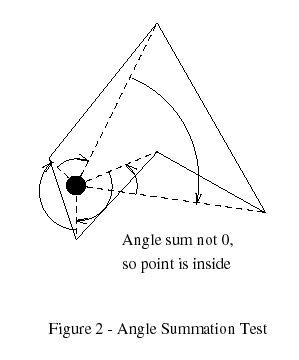
Angle Summation Test

The worst algorithm in the world for testing points is the angle summation method. It's simple to describe: sum the signed angles formed at the point by each edge's endpoints. If the sum is near zero, the point is outside; if not, it's inside (Figure 2). The winding number can be computed by finding the nearest multiple of 360 degrees. The problem with this scheme is that it involves a square root, arc-cosine, division, dot and cross product for each edge tested. In timing tests the MacMartin test was up to 63 times faster than the angle summation test for polygons with up to 100 sides. In fairness, the angle algorithm can be sped up in various ways, but it will still always be faster to use any other algorithm in this Gem.

Triangle Tests

In Graphics Gems, Didier Badouel (Badoeul 1990) presents a method of testing points against convex polygons. The polygon is treated as a fan of triangles emanating from one vertex and the point is tested against each triangle by computing its barycentric coordinates. As Berlin (Berlin 1985) points out, this test can also be used for non-convex polygons by keeping a count of the number of triangles which overlap the point; if odd, the point is inside the polygon (Figure 3). Unlike the convex test, where an intersection means that the test is done, all the triangles must be tested against the point for the non-convex test. Also, for the non-convex test there may be multiple barycentric coordinates for a given point, since triangles can overlap.

When the number of sides is small, the barycentric test is comparable to the MacMartin test in speed, with the additional bonus of having the barycentric coordinates computed. As the number of sides approached 100, the MacMartin test becomes 3 to 6 times faster than the barycentric method.

A faster triangle fan tester proposed by Green (Green 1993) is to store a set of half-plane equations for each triangle and test each in turn. If the point is outside any of the three edges, it is outside the triangle. The half-plane test is an old idea, but storing the half-planes instead of deriving them on the fly from the vertices gives this scheme its speed at the cost of some additional storage space. For triangles this scheme is the fastest of all of the algorithms discussed so far, being almost twice as fast as the MacMartin crossings test. It is also very simple to code and so lends itself to assembly language translation.

Both the half-plane and barycentric triangle testers can be sped up further by sorting the order of the edge tests. Worley and Haines (Worley 1993b) note that the half-plane triangle test is more efficient if the longer edges are tested first. Larger edges tend to cut off more exterior area of the polygon's bounding box, and so can result in earlier exit from testing a given triangle. Sorting in this way makes the test up to 1.6 times faster, rising quickly with the number of edges in the polygon. However, polygons with a large number of edges tend to bog down the sorted edge triangle algorithm, with the MacMartin test being from 1.6 to 2.2 times faster for 100 edge polygons.

For the general test a better ordering for each triangle's edges is to sort by the area of the polygon's bounding box outside the edge, since we are trying to maximize the amount of area discarded by each edge test. This ordering provides up to another 10% savings in testing time. Unfortunately, for the convex test below, this ordering actually loses about 10% for regular polygons due to a subtle quirk. As such, this ordering is not presented in the statistics section or the code.

Convex Polygons

Convex polygons can be intersected faster due to their geometric properties. For example, the crossings test can quit as soon as two Y sign difference edges are found, since this is the maximum that a convex polygon can have. Also, more polygons can be categorized as "convex" for the crossings test by checking only the change in the Y direction (and not X and Y as for the full convexity test). For example, a block letter "E" has at most two Y intersections for any test point's horizontal line, so it can be treated as convex when using the crossings test. Convexity is sufficient but not necessary for all of the algorithms discussed in this section.

The triangle fan tests can exit as soon as any triangle is found to contain the point. This algorithm can be enhanced by both sorting the edges of each triangle by length and also sorting the testing order of triangles by their areas. Larger triangles are more likely to enclose a point and so end testing earlier. Using both of these sorting strategies makes convex testing 1.2 times faster for squares and 2.5 times faster for regular 100 sided polygons.

Another strategy is to test the point against each exterior edge in turn. If the point is outside any edge, then the point must be outside the entire convex polygon. This algorithm uses less additional storage than the triangle fan and is very simple to code.

The order of edges tested affects the speed of the algorithm; testing edges which cut off the most area of the bounding box earliest on is the best ordering. Finding this optimal ordering is non-trivial, but doing the edges in order is often the worst strategy, since each neighboring edge usually cuts off little more area than the previous. Randomizing the order of the edges makes this algorithm up to 10% faster overall for regular polygons. However, even then the triangle fan algorithm with sorting is up to 1.35 times faster for 100 edge regular polygons.

The exterior edge strategy looks for an early exit due to the point being outside the polygon, while the triangle fan convex test looks for one due to the point being inside. For example, for 100 edge polygons if all points tested are inside the polygon the triangle fan is 1.7 times faster; if all are outside the exterior test is more than 11 times faster (but only 3 times faster if the edges are not randomized). So when the polygon/bounding box area is low the exterior edge strategy might be best.

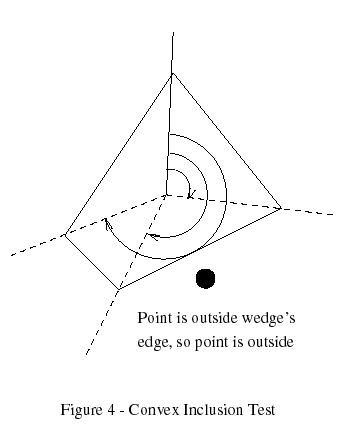
A method with O(log n) performance is discussed by Preparata and Shamos (Preparata 1985). The polygon is preprocessed by adding a central point to it and is then divided into wedges. The angles from an anchor edge to each wedge's edges are computed and saved, along with half-plane equations for each wedge's polygon edge. When a point is tested, the angle from the anchor edge is computed and a binary search is used to determine the wedge it is in, then the corresponding polygon edge is tested against it (Figure 4). This algorithm is slower for polygons with few edges because the startup cost is high, but the binary search makes for a much faster test when the number of edges is high.

Edge Problems

A problem that is sometimes important is determining if a point is exactly on an edge of a polygon. Being "exactly" on an edge entails computing error bounds and other issues in numerical analysis. While the "on" condition is of interest in CAD and elsewhere, for most computer graphics related operations this type of classification is unnecessary.

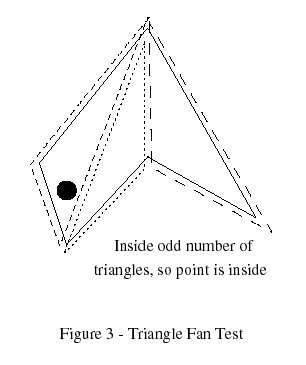
Problems occur in triangle fan algorithms when the code assumes that a point that lies on a triangle edge is inside that triangle. Points on the edges between test triangles will be classified as being inside two triangles, and so will be classified as being outside the polygon. This problem does not happen with the convex test. However, another problem is common to this family of algorithms. If a point is on the edge between two polygons, it will be classified as being inside both.

The code presented for these algorithms does not fully address either of these problems. In reality, a random point tested against a polygon using either algorithm has an infinitesimal chance of landing exactly on any edge. For rendering purposes this problem can be ignored, with the result being one mis-shaded pixel once in a great while.

The crossings test does not have these problems when the 2D polygons are in the same plane. By the nature of the test, all points are consistently categorized as being to one side of any given edge or vertex. This means that when a point is somewhere inside a mesh of polygons the point will always be in only one polygon. Points exactly on the unshared edge of a polygon will be classified as arbitrarily inside or outside the polygon by this method, however. Again, this problem is rarely encountered in rendering and so can usually be ignored.

Faster Tests

The algorithms presented so far for the general problem have been O(n); the order of the problem is related to the number of edges. Preparata and Shamos (Preparata 1985) present a fascinating array of solutions which are theoretically faster. However, these algorithms have various limitations and tend to bog down when actually coded due to expensive operations. In this section are some practical methods inspired by their presentation that perform well under ordinary circumstances. They are still O(n) for pathological cases, but for reasonable polygon data they are quite efficient. These methods use much more memory and have higher initialization times before testing begins, but are much faster per tested point.

Bins Method

One method to speed up testing is to classify the edges by their Y components and then test only those edges with a chance of intersecting the test point's X+ test ray. The bounding box surrounding the polygon is split into a number of horizontal bins and the parts of the edges in a bin are kept in a list, sorted by the minimum X component. The maximum X of the edge is also saved, along with a flag noting whether the edge fully crosses the bin's Y bounds. In addition, the minimum and maximum X components of all the edges in each bin are recorded.

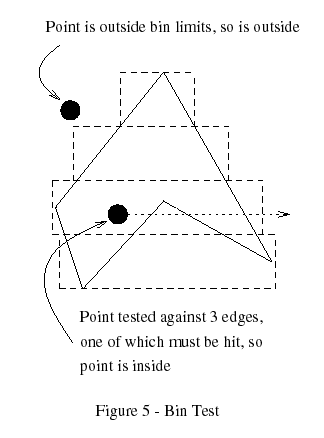
When a point is to be classified, the proper bin is retrieved and if the point is outside the X bounds, it must be outside the polygon. Else, the list is traversed and the edges tested against the point. Essentially, a modified crossings test is done, with additional speed coming from the sorted order and from the storage of the "fully crosses" condition (Figure 5).

Grid Method

An even faster, and more memory intensive, method of testing for points inside a polygon is using lookup grids. The idea is to impose a grid inside the bounding box containing the polygon. Each grid cell is categorized as being fully inside, fully outside, or indeterminate. The indeterminate cells also have a list of edges which overlap the cell, and also one corner (or more) is determined to be inside or outside using a traditional test. It is quick to determine the state of these corners by dealing with those on each latitude line by flipping the state of each corner to the right of the edge's crossing point.

To test a point against this structure is extremely quick in most cases. For a reasonable polygon many of the cells are either inside or outside, so testing consists of a simple look-up. If the cell contains edges, then a line segment is formed from the test point to the cell corner and is tested against all edges in the list (Antonio 1992). Since the state of the corner is known, the state of the test point can be found from the number of intersections (Figure 6).

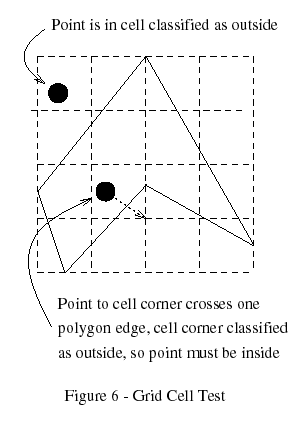
Care must be taken when a polygon edge exactly (or even nearly exactly) crosses a grid corner, as this corner is then unclassifiable. Rather than coping with the topological and numerical problems involved, one simple solution is to just start generating the grid from scratch again, giving slightly different dimensions to the bounding box. When testing the line segment against the edges in a list, exact intersections of an edge endpoint must be counted only once.

One additional speed up is possible. Each grid cell has four sides. If no edges cross a side, then that side will be fully inside or outside the polygon. A perfectly horizontal or vertical test line segment can then be generated and the faster crossings test can be used against the edges in the cell. The only test case where this made a significant difference was with a 20x20 grid imposed on a 1000 edge polygon, where the grid cell side test was 1.3 times faster.

Pixel Based Testing

One interesting case that is related to gridding is that of pixel-limited picking. When a dataset is displayed on the screen and a large amount of picking is to be done on a still image, a specialized test is worthwhile. Hanrahan and Haeberli (Hanrahan 1990) note that the image can be generated once into a separate buffer, filling in each polygon's area with an identifying index. When a pixel is picked on this fixed image, the point is looked up in this buffer and the polygon selected is known immediately.

Statistics

The following timings were produced on an HP 720 RISC workstation; timings had similar performance ratios on an IBM PC 386 with no FPU. The general non-convex algorithms were tested using two sorts of polygons: those generated with random points and regular (i.e. equal length sides and vertex angles) polygons with a random rotation applied. Random polygons tend to be somewhat unlikely (no one ever uses 1000 edge random polygons for anything except testing), while regular polygons are more orderly than a "typical" polygon; normal behavior tends to be somewhere in between. Convex-only algorithms were tested with only regular polygons, and so have a certain bias to them. Test points were generated inside the box bounding the polygon. Timings are in microseconds per test, and appear to be within roughly +-10% accuracy. However, the best way to get true timings is to run the code on the target machine; the code provided on disk has a test program which can be used to generate timings under various test conditions.

The performance of all the algorithms is practically linear; as such, the ratios of times for the 1000 edge polygons are representative of performance for polygons with a large number of edges.

General Algorithms, Random Polygons:

                       number of edges per polygon
                         3       4      10      100    1000
MacMartin               2.9     3.2     5.9     50.6    485
Crossings               3.1     3.4     6.8     60.0    624
Triangle Fan+edge sort  1.1     1.8     6.5     77.6    787
Triangle Fan            1.2     2.1     7.3     85.4    865
Barycentric             2.1     3.8    13.8    160.7   1665
Angle Summation        56.2    70.4   153.6   1403.8  14693

Grid (100x100)          1.5     1.5     1.6      2.1      9.8
Grid (20x20)            1.7     1.7     1.9      5.7     42.2
Bins (100)              1.8     1.9     2.7     15.1    117
Bins (20)               2.1     2.2     3.7     26.3    278

General Algorithms, Regular Polygons:

                       number of edges per polygon
                         3       4      10      100    1000
MacMartin               2.7     2.8     4.0     23.7    225
Crossings               2.8     3.1     5.3     42.3    444
Triangle Fan+edge sort  1.3     1.9     5.2     53.1    546
Triangle Fan            1.3     2.2     7.5     86.7    894
Barycentric             2.1     3.9    13.0    143.5   1482
Angle Summation        52.9    68.1   158.8   1489.3  15762

Grid (100x100)          1.5     1.5     1.5      1.5      1.5
Grid (20x20)            1.6     1.6     1.6      1.7      2.5
Bins (100)              2.1     2.2     2.6      4.6      3.8
Bins (20)               2.4     2.5     3.4      9.3     55.0

Convex Algorithms, Regular Polygons:

                       number of edges per polygon
                         3       4      10      100    1000
Inclusion               4.82    5.01    6.21     7.12     8.3

Sorted Triangle Fan     1.11    1.41    3.75    29.36   289.6
Unsorted Triangle Fan   1.25    2.04    6.30    69.18   734.7

Unsorted Barycentric*   1.79    2.80    6.94    65.62   668.7

Random Exterior Edges   1.11    1.61    3.82    33.44   333.6
Ordered Exterior Edges  1.28    1.70    4.15    41.07   408.9

Convex MacMartin        2.44    2.48    3.18    17.31   159.8

* The "unsorted barycentric" code is a slightly optimized version of Badouel's code in Graphics Gems (Badoeul 1990).

Summary

The statistics vary depending on the machine and implementation, but the general trends seem to hold. Avoid the angle summation test like the plague. For a general algorithm there are a few choices. Though it involves preprocessing and additional storage, the triangle fan test with edges sorted by length is the best for polygons with few edges. The barycentric test worth using for triangles and for when these additional coordinates are needed. The MacMartin test needs no additional memory or preprocessing and is good for polygons with a fair number of edges (the break point was around 7 to 9 edges vs. the triangle fan test on the HP 720) as is faster than the barycentric test for all but triangles.

Of the algorithms with efficiency structures, the trapezoid algorithm is somewhere in between the edge based algorithms and the gridding algorithm in speed. Gridding gives almost constant time performance for most normal polygons, though like the other crossings test it performs a bit slower when entirely random polygons are tested. Interestingly, even for polygons with just a few edges the gridding algorithm outperforms most of the other tests.

Testing times can be noticeably decreased by using an algorithm optimized for convex testing when possible. For example, the convex sorted triangle fan test is up to 2 times faster than its general case counterpart. For convex polygons with many edges the inclusion test is extremely efficient because of its O(log n) behavior. There is a zone from around 8 to 25 or so edges where the convex MacMartin test is slightly faster than the others, though not significantly so.

In summary, the basic crossings test is generally useful, but we can do better. Testing triangles using the sorted half-plane algorithm was more than twice as fast; on the other end of the spectrum, the MacMartin optimization made testing nearly twice as fast for polygons with many edges.

Code for this article is on the web.

References

(Antonio 1992) Antonio, Franklin, "Faster Line Segment Intersection," Graphics Gems III (David Kirk, ed.), Academic Press, pp. 199-202, 1992.

(Badouel 1990) Badouel, Didier, "An Efficient Ray-Polygon Intersection," Graphics Gems (Andrew S. Glassner, ed.), Academic Press, pp. 390-393, 1990.

(Berlin 1985) Berlin, E.P. Jr., "Efficiency Considerations in Image Synthesis," SIGGRAPH '85 course notes, volume 11, 1985.

(Glassner 1989) Glassner, Andrew S., ed., An Introduction to Ray Tracing, Academic Press, pp. 53-59, 1989. See Hypergraph for some related information.

(Green 1993) Green, Chris, "Simple, Fast Triangle Intersection," Ray Tracing News 6(1), 1993.

(Hanrahan 1990) Hanrahan, Pat and Haeberli, Paul, "Direct WYSIWYG Painting and Texturing on 3D Shapes," Proceedings of SIGGRAPH 90, 24(4), pp. 215-223, August 1990.

(MacMartin 1992) MacMartin, Stuart, et al, "Fastest Point in Polygon Test," Ray Tracing News 5(3), 1992.

(Preparata 1985) Preparata, F.P., and Shamos, M.I., Computational Geometry, Springer-Verlag, New York, pp. 41-67, 1985.

(Schorn 1994) Schorn, Peter, and Fisher, Frederick, "Testing the Convexity of a Polygon," Graphics Gems IV, (ed. Paul Heckbert), p. 7-15, 1994.

(Shimrat 1962) Shimrat, M., "Algorithm 112, Position of Point Relative to Polygon," CACM, p. 434, August 1962.

(Woo 1992) Woo, Andrew, "Ray Tracing Polygons using Spatial Subdivision," Proceedings of Graphics Interface '92, pp. 184-191, 1992.

(Worley 1993a) Worley, Steve and Haines, Eric, "Bounding Areas for Ray/Polygon Intersection," Ray Tracing News 6(1), 1993.

(Worley 1993b) Worley, Steve and Haines, Eric, "Triangle Intersection Revisited," Ray Tracing News 6(2), 1993.

Last change: July 31, 2001

Eric Haines / erich@acm.org